RSS News

Solar Technologies

What is Solar?

Photovoltaic Electronic Generator

Solar Hot Water Heater

Solar Panel

Photovoltaic Solar Cells

Commercial Solar Lighting

Upcoming Seminars

Solar Theory

Photoelectric Effect

The photoelectric effect is a quantum electronic phenomenon in which electrons are emitted from matter after the absorption of energy from electromagnetic radiation such as x-rays or visible light.[1] The emitted electrons can be referred to as photoelectrons in this context. The effect is also termed the Hertz Effect,[2][3] due to its discovery by Heinrich Rudolf Hertz, although the term has generally fallen out of use.

Photoelectric effect


A diagram illustrating the emission of electrons from a metal plate, requiring energy gained from an incoming photon to be more than the work function of the material.
Light-matter interaction
Low energy phenomena	Photoelectric effect
Mid-energy phenomena	Compton scattering
High energy phenomena	Pair production

Photoelectric effect takes place with photons with energies of about a few eV. If the photon has sufficiently high energy, Compton scattering(~keV) or Pair production(~MeV) may take place.

Study of the photoelectric effect led to important steps in understanding the quantum nature of light and electrons and influenced the formation of the concept of wave–particle duality.[1]

The term may also refer to the photoconductive effect (also known as photoconductivity or photoresistivitity), the photovoltaic effect, or the photoelectrochemical effect.

3 History

4 Uses and effects

5 References

Introduction

When a metallic surface is exposed to electromagnetic radiation above a certain threshold frequency, the light is absorbed and electrons are emitted. In 1902, Philipp Eduard Anton von Lenard observed that the energy of individual emitted electrons increased with the frequency, or colour, of the light. This was at odds with James Clerk Maxwell's wave theory of light, which predicted that the quantized vacuum-energy would be proportional to the intensity of the radiation. In 1905, Einstein solved this paradox by describing light as composed of discrete quanta, now called photons, rather than continuous waves. Based upon Max Planck's theory of black-body radiation, Einstein theorized that the energy in each quantum of light was equal to the frequency multiplied by a constant, later called Planck's constant. A photon above a threshold frequency has the required energy to eject a single electron, creating the observed effect. This discovery led to the quantum revolution in physics and earned Einstein the Nobel Prize in 1921.

Explanation

The photons of the light beam have a characteristic energy determined by the frequency of the light. In the photoemission process, if an electron absorbs the energy of one photon and has more energy than the work function (the electron binding energy), it is ejected from the material. If the photon energy is too low, the electron is unable to escape the surface of the material. Increasing the intensity of the light beam increases the number of photons in the light beam, and thus increases the number of electrons emitted without increasing the energy that each electron possesses. Thus the energy of the emitted electrons does not depend on the intensity of the incoming light, but only on the energy of the individual photons.

Electrons can absorb energy from photons when irradiated, but they follow an "all or nothing" principle. All of the energy from one photon must be absorbed and used to liberate one electron from atomic binding, or the energy is re-emitted. If the photon energy is absorbed, some of the energy liberates the electron from the atom, and the rest contributes to the electron's kinetic energy as a free particle

Explanation

For a given metal and frequency of incident radiation, the rate at which photoelectrons are ejected is directly proportional to the intensity of the incident light.
For a given metal, there exists a certain minimum frequency of incident radiation below which no photoelectrons can be emitted. This frequency is called the threshold frequency.
Above the threshold frequency, the maximum kinetic energy of the emitted photoelectron is independent of the intensity of the incident light but depends on the frequency of the incident light.
The time lag between the incidence of radiation and the emission of a photoelectron is very small, less than 10-9 second.

Equations

In effect quantitatively using Einstein's method, the following equivalent equations are used:
Energy of photon = Energy needed to remove an electron + Kinetic energy of the emitted electron
Algebraically:
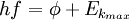
$hf = \phi + E_{k_{max}} \,$
where

h is Planck's constant,
f is the frequency of the incident photon,
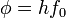$\phi = h f_0 \$ is the work function (sometimes denoted W instead), the minimum energy required to remove a delocalised electron from the surface of any given metal,
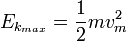$E_{k_{max}} = \frac{1}{2} m v_m^2$ is the maximum kinetic energy of ejected electrons,
f0 is the threshold frequency for the photoelectric effect to occur,
m is the rest mass of the ejected electron, and
vm is the speed of the ejected electron.

Since an emitted electron cannot have negative kinetic energy, the equation implies that if the photon's energy (hf) is less than the work function (φ), no electron will be emitted.
According to Einstein's special theory of relativity the relation between energy (E) and momentum (p) of a particle is 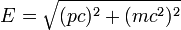$E = \sqrt{(pc)^2 + (mc^2)^2}$ , where m is the rest mass of the particle and c is the velocity of light in a vacuum.

Three-step model

The photoelectric effect in crystalline material is often decomposed into three steps:[4]

Inner photoelectric effect (see photodiode below). The hole left behind can give rise to auger effect, which is visible even when the electron does not leave the material. In molecular solids photons are excited in this step and may be visible as lines in the final electron energy. The inner photoeffect has to be dipole allowed. The transition rules for atoms translate via the tight-binding model onto the crystal. They are similar in geometry to plasma oscillations in that they have to be transversal.
Ballistic transport of half of the electrons to the surface. Some electrons are scattered.
Electrons escape from the material at the surface.

In the three-step model, an electron can take multiple paths through these three steps. All paths can interfere in the sense of the path integral formulation. For surface states and molecules the three-step model does still make some sense as even most atoms have multiple electrons which can scatter the one electron leaving.

Copyrights © 2008 Florida Solar Energy. All rights reserved.
Florida Solar Energy L 1700 S. Dixie Highway, Boca Raton FL 33432.
561-206-2324 P 561-207-7807 F info@floridasolarenergy.com
www.floridasolarenergy.com

Website Designed by Intranet-Services